Expertise:
Beginner
What is a basis function?
Here's the problem. We want a mathematical description of a curve
or any other data distributed over space, time, and other types of continuum.
Flexibility is a central issue since we usually cannot say in advance
how complex the curve will be, or specify certain of its characteristics.
We don't have the time or patience to search some handbook of known functions for
one that looks like what we want to study, either. Moreover, however
it is that we design our mathematical function, we will want to do any computation that
is needed to fit the data quickly and with a minimum of programming.
We need, therefore, a set of basic functional building blocks that
can be stacked on top of one another so as to have the features
that we need. Mathematical Lego, Meccano, Erector, Tinker Toy, or whatever, in other
words. Since this is mathematics, we use the symbol øk(t)
to stand for the kth function in our toy box, and we call this the kth basis function.
By "stacking" in mathematics we mean adding things, possibly after multiplying
each of them by its own constant. So here is how we will construct a function
f(t) using K of these blocks:
f(t) = a1ø1(t) + a2ø2(t) +
.... + akøk(t)
In math-speak, this is a "linear combination". The construction of an actual
function then becomes a matter of assigning values to the Κ constants
ak.
What are some examples of commonly used basis functions?
There are many ways to put together a kit of basis functions. The oldest system consists
of the powers of t, that is, 1, t, t2, ... , tk.
Linear combinations of these functions are called polynomials.
A system developed in early nineteenth century France is the Fourier
basis, consisting of 1 and a series of pairs of sines and cosines
of increasing frequency; that is, 1, sin(ωt), cos(ωt),
sin(2ωt), cos(2ωt), sin(3ωt), cos(3ωt),....
The constant ω plays an important role: functions constructed with
this system repeat themselves each time t increases by 2π/ω units.
Consequently, we tend to use this basis for periodic functions.
Figure 1 shows the first five basis functions in the series with a period of one unit.
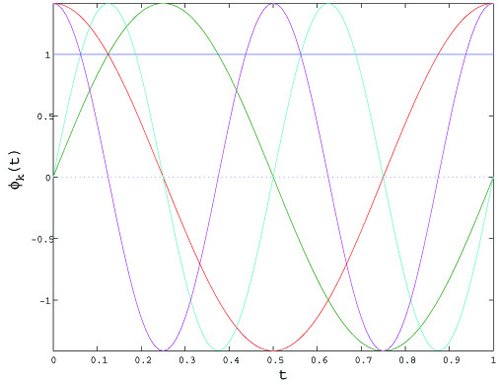
Figure 1: The first five functions in the Fourier series with a period of one unit.
Polynomials, though simple and familiar, are actually not that flexible, and consequently
they have been more or less replaced by a basis system called the
spline basis system. Splines, although related to polynomials systems,
require some further explanation, and we have some special notes
on them in this website. However, you can have a preliminary look
at spline basis functions in figure 2. There are plenty of other
basis systems around, and it is worth mentioning wavelets at this point,
without ordering any description of this system in these introductory notes.
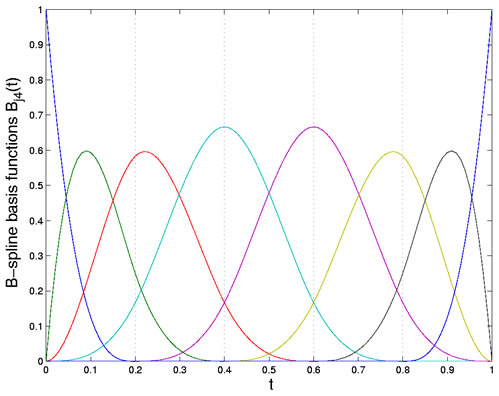
Figure 2: The eight B-spline basis functions of order four defined by the breakpoints shown as dotted lines.
|

