Expertise:
Beginner
What's wrong with fitting the data exactly?
If the data are highly accurate, and if only the curve fitting the data itself
is required, there's nothing at all wrong with this. But if you are going to do
more than just display the functional data object, even a small amount of noise
can cause problems.
For example, Figure 1 shows the velocity or rate of change of height
for the first 10 Berkeley girls as calculated from the curves calculated
in the From Raw Data
to Functional Data web page, where the raw data were fit exactly.
We see that these velocity curves are distressingly wiggly, and it's hard
to believe that growth
velocity changes that much. Probably, we imagine, this is due to
the impact of a measurement area of around three centimeters on the
velocity curves. This is
true; even a small amount of wiggle in a curve is greatly magnified
in computing its rate of change or first derivative.
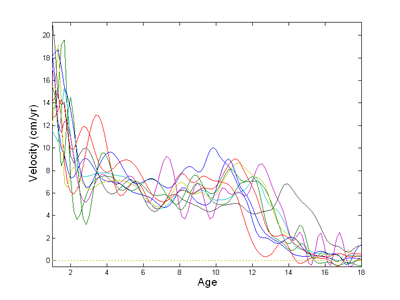
Figure 1: The rate of change or velocity of height calculated from the height
curves calculated without smoothing for the first 10 Berkeley girls.
These velocities are too rough to be either plausible or useful.
How can I get rid of the noise in the fitted curve?
You can never get rid of it entirely, of course. But if we are right to assume
that the underlying process producing the data is smooth, then we can do much
better by also forcing the fitted curve to be smooth.
A common method for forcing a curve to be smooth is to penalize the curve's
curvature. See Ramsay and Silverman (1997) for a discussion of how to do this.
Now the curvature of a curve at a point is essentially
equivalent to its second derivative or acceleration at that point. For example, if
a curve is a straight line, than acceleration or the second derivative is exactly
zero everywhere, and the curve has no curvature anywhere.
We define the total curvature of the curve as the square of the second derivative
summed or integrated across the whole curve. This measures the roughness
of the curve.
Here, though, we will want to look at acceleration curves. These are themselves
second derivatives. What we want to do, therefore, is penalize the curvature
in the second derivative. It follows that what we should really control is
the roughness of the fourth derivative, the curvature of the accleration, in other
words.
|