Expertise:
Intermediate
How does this smoothing operation work(continued)?
Can we do this again? Of course. You may need to sketch how how this
works for yourself, and you can consult Figure 3, below, for a plotted
version.
-
multiply the tent function on the left by the same tilt function that
we used on the box function.
-
make a copy of the tent function and shift it one unit to the right,
so that it's right side goes to zero at t = 3.
-
multiply by the tilt function whose value is 3 - t, t ≤ 3,
and 0 elsewhere.
-
lastly, add the left-tilted original tent, and the right-tilted shifted
copy.
If your sketch is on track, you will see what you now have a function
composed of three quadratic segments. Moreover, these segments will
not only have values that match at the two breakpoints at t = 1 and t = 2, but they will
also have matching slopes or first derivatives. They will now, in fact, look quite smooth.
Perhaps we can call this a bulge function. Note, too, that the function will also approach zero
on both the right and the left with value and slope going to zero. Figure 3 shows in its three
panels how this mother spline function of order 3 is constructed.
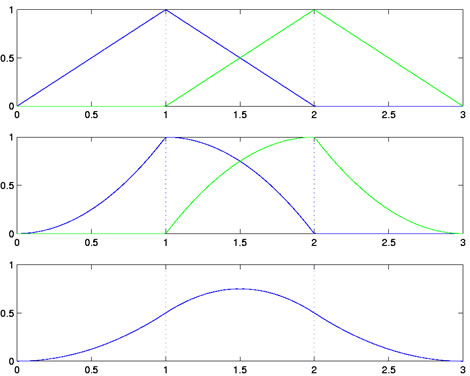
Figure 3: The three steps to constructing the mother basis spline of order 3, shown in the bottom panel,
from the mother basis spline of order 2 and a right shifted version, shown in the top panel.
Hopefully you now have the idea in hand. You'll have to be a rather expert drafts-person to plot
the result of left-tilting the bulge, right-tilting its right-shifted copy, and adding the two components,
or perhaps you will prefer to do the math instead, but either way, you will now see the typical basis
function for a cubic smoothing spline. It will extend from t = 0 to t = 4, have three
breakpoints, and have matching values, slopes, and second derivatives at each of these breakpoints
as well as at 0 and 4.
Isn't there an elegant formula for all this?
There sure is. It is a recursion formula, and it works by showing how two adjacent spline functions
of a particular order are combined together to get a single new basis function of order one higher.
First we need some notation. Let Bjm(t) indicate the value of a spline basis function of
order m with a left side where it first rises from zero at t = j. This function is defined
for any value of t, but the basis function will only be positive with the successive m
subintervals beginning at t = j, and otherwise will be zero. For example, our original mother
box function is B01(t), and is only positive for 0 ≤ t < 1. The tent function that we
constructed above is B12(t). The notation B11(t) is used for a right-shifted
mother box function with left side at t = 1. The mother cubic spline function is B04(t),
and B54(t) is the result of shifting this function 5 places to the right. Of course, there's
no reason why we can't shift to the left, too, so that B-1,1 is a left-shifted
mother box.
Here, then is the recursion:
(m - 1)Bjm(t) = (t - j)Bj,m-1(t)
+ (m + j - t)Bj+1,m-1(t)
You can see the recursion formula the left-side tilting operation in the multiplication of the first term
on the left side by (t - j), the right-side tilting in the factor (m + j - 1)
in the second term, and of course the final summation.
Actually, the recursion adds one new thing to our geometric description above by multiplying the left side
by the factor m - 1. This is not entirely necessary, but it does keep the spline basis functions
from growing taller and taller as we increase their order. Spline basis functions constructed with this
factor on the left side are called B-spline basis functions, where the "B" was
used by their inventor, C. de Boor, to stand for "basis".
What about breakpoints that are not integers?
By using only integers as breakpoints, we have been able to keep
things simple enough so that we hopefully see what is going on in
these three operations, namely shifting, scaling, and
smoothing. However, these same operations have their counterparts
when breakpoints are positioned at any sequence ξ1 < ξ2 < .
. . < ξL.
The more general recursion is then:
(m - 1)Bjm(t) = (t - ξj)Bj,m-1(t)
+ (ξj+m - t)Bj+1,m-1(t)
Thus, the shift and scaling parts of the process are determined more generally by the spacing of the breakpoints.
But what happens at the endpoints tL and tU?
We can take care of the basis functions at the end points by extending the breakpoint sequence beyond both the left
and right boundaries, and then only using that segments of the resulting spline basis functions that fall within the
interval that we are using. It does not matter how we extend this sequence, since we ignore the behavior of the basis
functions outside of the interval, and their shapes within the interval are essentially not affected by what they do outside.
|
