This page provides a brief tutorial for the confidence interval calculator described in Falk & Biesanz (2016). The program is intended to be easy-to-use, does not require commercial statistical software, does not require editing of SPSS or SAS syntax, and does not require the raw data.The user only needs to input information that one would normally need to obtain anyway if performing mediational analysis using traditional methods (e.g., regression coefficients, standard errors, degrees of freedom, and t-statistics).
Within the program, there are two computational methods - one method where sampling distributions are based in-part on posterior (and t) distributions (appropriate for regression models), and a second method where normal approximations are used in place of posterior distributions (appropriate for larger samples or methods where such normal approximations are used, such as structural equation models).
Confidence intervals are available from the hierarchical Bayesian (appropriate for multiple regression models) and Monte Carlo methods (appropriate for structural equation and some multilevel models - see FAQ on use of some multilevel models). In Biesanz et al (2010), the hierarchical Bayesian method provided coverage rates for the indirect effect that outperformed both the distribution of the product method and the BCa bootstrap. The Monte Carlo method performs similarly to the hierarchical Bayesian method and distribution of the product method at large sample sizes. The Monte Carlo method is also appropriate for confidence intervals in structural equation models as it allows for a correlation between the two paths in the model (which is not necessarily 0 in models that contain latent variables).
Users of the confidence interval calculator calculator may cite:
Falk, C.F., & Biesanz, J.C. (2016). Two cross-platform programs for inferences and interval estimation about indirect effects in mediational models. SAGE Open, 6. http://dx.doi.org/10.1177/2158244015625445
Instructions on program use
Click on the link below to download the program.
MediationCI.jar (last update: 2015-08-18)
Once downloaded, double click on the file and it will open in a new window. For some users, it may require an update/install to a new version of Java Runtime Environment: https://java.com/en/download/
This program is computationally intensive. So far the program has been tested under Windows XP, Windows 7, and OSX (Mac) version 10.7.3 (Lion). If you encounter any problems with the program, please report them directly to me: carl.falk@mcgill.ca
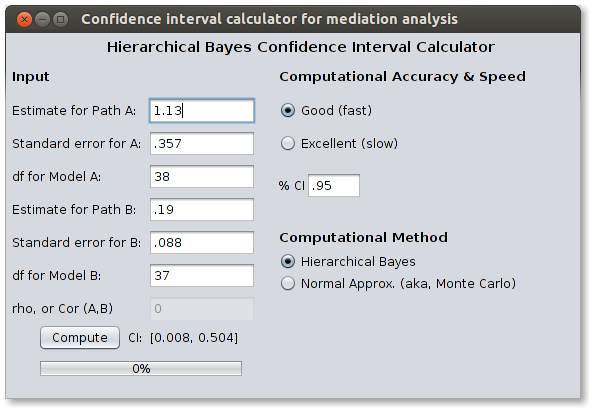
After the program loads, the next step is to enter the regression coefficient, standard error, and degrees of freedom for the a path in the mediational model. In the empirical example in Biesanz, Falk, and Savalei (2010), these values are 1.13, .357, and 38, respectively. After that, enter the regression coefficient, standard errors, and degress of freedom for the b path in the mediational model. In the empirical example in Biesanz, Falk, and Savalei (2010), these values are .19, .088, and 37. The result of these two steps is shown below. If the paths are part of a structural equation model, omit the df, select “Normal approx.” as the computational method, and enter the correlation between the two paths of the model (obtained from the variance-covariance matrix of model parameters).
Next click “Compute” and the program will get to work. Note that “Good” computational accuracy will usually take just a couple minutes and is recommended for general use. Researchers wishing a higher level of stability (e.g., confidence intervals that vary less from run to run) for publication may use the “Excellent” computational accuracy setting, but must be prepared to be very patient.
The result of the program is now displayed below. The confidence interval does not contain zero, but includes values from .008 to .504.